Hvordan finne vinkelen mellom vektorer?

Vinkelen mellom de to vektorene som går medett punkt er nærmeste vinkel, en rotasjon der den første vektoren rundt sin opprinnelse vil føre den til posisjonen til den andre vektoren. Men hvordan finner du vinkelen mellom vektorene? Vår artikkel vil fortell om dette.
Vi har to ikke-nullvektorer som kommer fra et enkelt punkt - en vektor A som har koordinater (x1, y1), vektoren B har koordinatene (x2, y2). Vinkelen mellom dem er μ.
- Vi bruker definisjonen av et skalarprodukt for å finne graden av vinkelen μ. Vi oppnår (A, B) = | A | * | B | * cos (μ). Vi uttrykker cosinus av vinkelen. Og så cos (μ) = (A, B) / (| A | * | B |).
- Den kan også bli funnet med formelen: (A, B) = x1* x2 + y1* y2. Når vektørens skalære produkt ernull - vektorene er vinkelrette (vinkelen mellom dem er 90 °), slik at det ikke utføres ytterligere beregninger. Hvis skalarproduktet har et positivt tegn, er vinkelen mellom vektorene akutt, dersom negativt tegn er en stump vinkel.
- Videre antar vi at lengdene av vektorene A og B er gitt ved formlene | A | = v (x1² + y1²), | B | = v (x2² + y2²). Vektors lengder er kvadratrøttene av summene av rutene i koordinatene sine.
- Verdiene funnet for søke av lengdene av vektorene og skalar produkt av den resulterende erstatning i trinn 2 i formelen, noe som gjør det mulig å finne den cosinus til vinkelen. Vi har: cos (μ) = (x1* x2 + y1* y2) / (v (x1² + y1²) + v (x2² + y2²)).
- Har cosinusverdien for å finne vinkelen mellomvektorer av, vi bruker Bradys bordet. Også for dette kan du ta arccosinen. Da får vi μ = arccos (cos (μ)). Bradysbordet kan sees, for eksempel her: www.math.com.ua.
For å finne vinkelen mellom vektorene på nettet, kan du for eksempel bruke slike lenker: www.ru.onlinemschool.com og www.mathserfer.com.
Les mer:
Hvordan finne volumet av en parallellpiped?

Hvordan finne området for en firkant?
Hvordan finne høyden på en diamant?
Hvordan finne vinklene til en likemessig trekant?

Regelen av venstre hånd
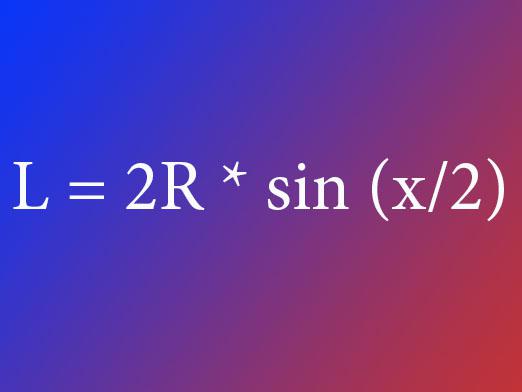
Hvordan finne en akkord?

Hvordan finne en sinus hvis cosinus er kjent?
Hvordan finne radiusen til den omkretsede sirkelen?
Hvordan finne katetre?

Hvordan finne området for et parallellogram?