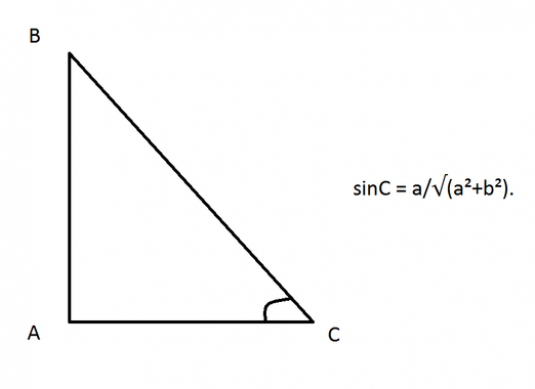Hvordan finne en sinus?

Se på videoen

Studien av geometri bidrar til å utvikle tenkning. Dette emnet kommer nødvendigvis inn i skolens forberedelse. I livet kan kunnskap om dette emnet komme til nytte - for eksempel når du planlegger en leilighet.

Fra historien

I rammen av geometriforløpet studeres også trigonometri, som utforsker trigonometriske funksjoner. I trigonometri studerer vi sines, cosines, tangenter og cotangents av vinkelen.

Men for øyeblikket begynner vi med det enkleste - sinus. La oss se nærmere på det aller første konseptet - sinus av en vinkel i geometri. Hva er en sinus og hvordan finner du den?

Begrepet "sinusvinkel" og sinusoider

Vinkelen av en vinkel er forholdet mellom verdienedet motsatte benet og hypotenusen til en rettvinklet trekant. Dette er en direkte trigonometrisk funksjon, som i brevet er betegnet som "sin (x)", hvor (x) er trekantenes vinkel.

På grafen er sinusens vinkel betegnet av en sinusoid ωdens funksjoner. Sinebølgen ser ut som en kontinuerlig bølgelignende linje som ligger i en viss ramme på koordinatplanet. Funksjonen er merkelig, derfor er den symmetrisk om 0 på koordinatplanet (det etterlater opphavsadressen til koordinatreferansen).

Domenet til definisjon av denne funksjonen ligger ivarierer fra -1 til +1 på et kartesisk koordinatsystem. Perioden for sinus-hjørnefunksjonen er 2 Pi. Dette betyr at hvert 2 Pi mønster gjentas, og sinusbølgen går gjennom en full syklus.

Ligning av en sinusoid

synd x = a / c
hvor a er katete motsatt hjørnet av trekanten
c - hypotenusen til en rettvinklet trekant

Angle Sine Properties

synd (x) = - synd (x). Denne funksjonen demonstrerer at funksjonen er symmetrisk, og hvis vi setter verdiene for x og (-x) på begge sider av koordinatsystemet, vil ordinatene til disse punktene være motsatt. De vil være like langt fra hverandre.
En annen funksjon av denne funksjonen er at,at grafen av funksjonen øker på intervallet [-Π / 2 + 2 Пn]; [П / 2 + 2Пn], hvor n er et heltall. Nedgangen i vinkelen sinus vil bli observert på segmentet: [П / 2 + 2 Пn]; [3P / 2 + 2Pn].
synd (x)> 0, når x ligger i området (2πn, Π + 2πn)
(x) <0, når x er i området (-Pr + 2Pn, 2Pn)

Verdiene av vinkelsynene bestemmes av spesielletabeller. Slike tabeller er opprettet for å lette beregningen av komplekse formler og ligninger. Det er enkelt å bruke og inneholder ikke bare funksjonene synd (x), men også verdiene til andre funksjoner.

Videre er tabellen over standardverdier av disseFunksjoner er inkludert i obligatorisk minnestudie, som multiplikasjonstabell. Dette gjelder spesielt for klasser med fysisk og matematisk bias. I tabellen kan du se verdiene for hovedvinklene som brukes i trigonometri: 0, 15, 30, 45, 60, 75, 90, 120, 135, 150, 180, 270 og 360 grader.

verdi av vinkel a (grader)	15	30	45	60	75	90	120	135	150	180	270	360
Verdien av vinkelen a i radianer (i form av tallet pi)	π / 12	π / 6	π / 4	π / 3	5π / 12	π / 2	2π / 3	3π / 4	5π / 6	π	3π / 2	2π
synd (sinus)	√3-1 / 2√2	1/2	√2 / 2	√3 / 2	√3 + 1 / 2√2	1	√3 / 2	√2 / 2	1/2	0	-1	0

Det er også et bord som definerer verdienetrigonometriske funksjoner av ikke-standard vinkler. Ved å bruke forskjellige tabeller kan du enkelt beregne sinus, cosinus, tangent og cotangent av noen vinkler.

Med trigonometriske funksjoner blir kompilertEq. For å løse disse ligningene får vite om enkle trigonometriske identiteter og kjørefunksjoner, for eksempel sin (n / 2 + x) = cos (x) og andre. For slike spøkelser er det også opprettet et eget bord.

Hvordan finne sinus av en vinkel

Når oppgaven er å finne sinusen av en vinkel, og forutsatt at vi bare har cosinus, tangent eller cotangent av vinkelen, kan vi enkelt beregne ønsket ved hjelp av trigonometriske identiteter.

synd²x + cos²x = 1

Basert på denne ligningen finner vi både sinus og cosinus, avhengig av hvilken verdi som er ukjent. Vi får en trigonometrisk likning med en ukjent:

synd²x = 1 - cos²x
synd x = ± √ 1 - cos²x
CTG²x + 1 = 1 / sin²x

Fra denne ligningen kan du finne verdien av sinusen, å vite verdien av vinkelen cotangent. For enkelhet, erstatt synd²x = y, og så får du en enkel ligning. For eksempel er verdien av cotangent 1, da:

1 + 1 = 1 / y
2 = 1 / y
2y = 1
y = 1/2

Gjør nå omvendt erstatning av spillet:

synd²x = ½
synd x = 1 / √2

Siden vi tok cotangentverdien for standardvinkelen (45⁰), kan verdiene som er oppnådd, kontrolleres fra bordet.

Hvis du får verdien av en tangent, og du må finne en sinus, vil en annen trigonometrisk identitet hjelpe:

tg x * ctg x = 1

Av dette følger at:

ctg x = 1 / tg x

For å finne en sinus med en ikke-standard vinkel, for eksempel 240⁰, er det nødvendig å bruke formlene for å redusere vinklene. Vi vet at π tilsvarer 180⁰. Dermed uttrykker vi vår likestilling ved hjelp av standardvinkler ved nedbrytning.

240⁰ = 180⁰ + 60⁰

Vi må finne følgende: synd (180⁰ + 60⁰). I trigonometri er det reduksjonsformler, som i dette tilfellet er nyttige. Dette er formelen:

synd (π + x) = - synd (x)

Dermed er sinus av vinkelen på 240 grader lik:

synd (180⁰ + 60⁰) = - synd (60⁰) = - √3 / 2

I vårt tilfelle, x = 60 og P, henholdsvis 180 grader. Verdi (-√3 / 2) fant vi fra tabellen over verdier av funksjoner av standardvinkler.

På denne måten kan ikke-standard vinkler utvides, for eksempel: 210 = 180 + 30.

I lærebøker og Internett kan du møte mangeformler for å beregne trigonometriske ligninger - subtraksjon, tillegg, produkt og deling av trigonometriske funksjoner av forskjellige vinkler til hverandre, oppstigning til kraften og omformingen av en funksjon til en annen ved hjelp av enkle identiteter og mange andre operasjoner.

For mer informasjon om sines og cosines, se: