Hvordan finne sinus av vinkelen til en trekant?
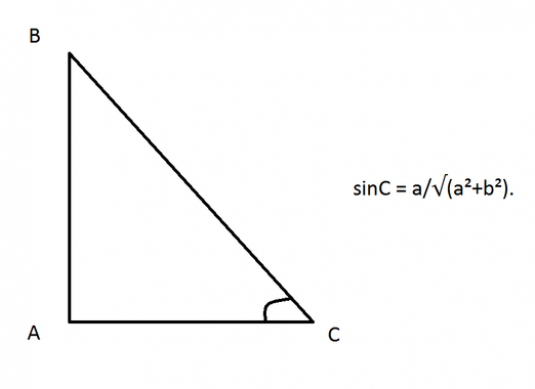
For å finne sinus av vinkelen til en rektangulær trekant, må vi huske hva en sinus er per definisjon. Og definisjonen er veldig enkel: Vinkelen sinus er lik forholdet mellom det motsatte benet til hypotenusen.
Hvordan beregne sines
Hvis vi har en trekant ABC, for hvilken A -En rett vinkel, så sidene AB og AC blir bena, og siden BC - hypotenuse. Derfor er sinus av vinkelen B per definisjon lik forholdet mellom benet til AC til hypotenusen: sinB = AC / BC, og sinusen til den andre vinkelen sinC = AB / BC.
I en rettvinklet trekant, funksjonene til vinkleneDet er praktisk å beregne: ingen ekstra konstruksjoner er nødvendig. Det er nok å kjenne lengden på høyre side. Men oftere bare en del av de nødvendige dataene er kjent, resten skal søkes. Vurder hvordan du gjør dette.
Leter etter en sinus med to ben
Vi tar den samme trekant ABC med riktig vinkel A, der vi kjenner benens dimensjoner: AB = a, AC = c. For å beregne sinusen i vinkel C, er det nødvendig å dele katete i en hypotenuse:
- sinC = AB / BC = a / BC (1).
Men hypotenusen må vurderes i henhold til pythagorasetningen:
- BC = √ (AB² + AC²) = √ (a² + b²). (2)
Vi leverer den funnet verdien av hypotenusen (2) i uttrykk (1), vi får svaret:
- sinC = a / √ (a² + b²).
Leter etter en sinus på hypotenusen og det tilstøtende benet
Nå, i samme trekant, må vi finne sinus av samme vinkel C, men vi vet hypotenusen BC = b og katoden AC = c. Med hjelp av Pythagorasetningen: AB² + AC² = BC² ser vi etter AB:
- AB = √ (b²-c²).
Bytt nå den funnet verdien av AB i formelen for sinusen:
- sinC = AB / b = √ (b²-c²) / b.
Sinberegning på den ene siden og skarpt hjørne
I trekanten ABC med rett vinkel A er vinkelen B = β kjent, og katetesen AC = c. Vi må finne sinus av vinkelen C.
Metode 1.
Den enkleste - hvis du husker at summen av alle vinklene i trekanten er 180 °:
- A + B + C = 180 °.
- Vinkelen A = 90 °, B = β,
- C = 180 ° -90 ° - β = 90 ° - β.
- Derfor sinC = sin (90 ° - β).
Metode 2.
Men du kan gå den andre veien:
- Sinβ = AC / BC; Sinβ = c / BC. Herfra:
- BC = c / Sinβ.
Fra ordet Pythagoras AB2 + AC2 = BC2 finner vi hypotenusen:
- AB = √ (BC²-AC²).
Vi erstatter de kjente verdiene:
- AB = √ (с² / Sin²β-c²) = √с² (1 / Sin²β-1) = с√ (1 / Sin²β-1).
Derfor finner vi sinus av vinkelen C:
- sinC = AB / BC = c√ (1 / Sin²β-1) / s / Sinβ = Sinβ √ (1 / Sin²β-1)
svare:
- sinC = Sinβ √ (1 / Sin²β-1).









