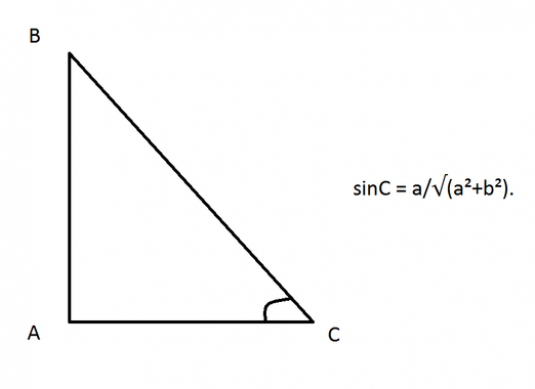Hva er en sinus?

Hvem blant oss ropte ikke på skolen som matematikk til hamaldri nyttig. Det virket for oss alle at alle disse abstruse formler, besværlige ligninger og komplekse navn har ingenting å gjøre med det virkelige liv. Men før eller senere all den kunnskapen vi fikk på skolen finner sin søknad. Og å vite hva en sinus, cosinus eller tangent kan redde ditt omdømme.

Litt av skolen geometri

Så er sinus aspektforholdet i en rettvinklet trekant. La oss huske hva den rektangulære trekanten består av.

Hjørner. Summen av vinklene i trekanten er 180^omtrent. Forovervinkelen er 90^omtrent. Derfor skal de andre to i summen også gi 90^omtrent. Det vil si at vi har en rett vinkel og to skarpe.

Fest. Den rektangulære trekant består av en hypotenuse og to ben. To bein danner en rett vinkel, og hypotenusen ligger motsatt den.

Hva er sinus av en vinkel? Som allerede nevnt, dette aspektforholdet. Men hvilke? Sinken i en skarp vinkel er forholdet mellom benet, som ligger overfor denne vinkelen, til hypotenusen. Tenk på eksemplet:

Sine av vinkel A er forholdet mellom side a (motsatt ben) til side b (hypotenuse).

Sine av vinkel C er sideforholdet med (katete ligger motsatt side C) til side b (hypotenuse).

Det vil si at hvis sidene er lik a = 3, c = 4, b = 5, vil sinus av vinkel A være 3/5, og sinus av vinkel C vil være 4/5.

Hva gir dette oss? Så langt, ingenting, men la oss se på et annet eksempel. La oss øke trekanten ved å utvide sidene. Nå har vi gjort dette:

Som det fremgår av figuren, økte sidelengdene, men hjørnene gjorde det ikke. Men det som er mest interessant - forholdet endret seg heller ikke!

Anta, d = 6, k = 8, m = 10. Så er sinus av vinkelen A d / m = 6/10. Vi kutter det ved to sider av ligningen og får det samme 3/5, som i det første tilfellet! Og uansett hvordan du endrer, utvider eller forkorter partiene, vil partiets holdning fortsatt være den samme.

Derfor er det klart at sinusen er en konstant verdi.

Og nå - trigonometri

De gamle grekerne la merke til dette i lang tid. De kalkulerte bihulene i hovedhjørnene og registrerte dem for å fortsette å bruke allerede klare mengder, og ikke å oppfinne nye.

I tillegg til sinusen har vinkelen også en cosinus(forholdet til det tilgrensende benet til hypotenusen), tangenten (forholdet mellom det motsatte benet og den tilstøtende) og cotangenten (forholdet mellom det tilstøtende beinet til motsatt). Alle disse mengdene kalles trigonometriske funksjoner av vinkelen, og brukes til beregninger og problemløsing.

Mystiske bord av Bradys

Hver gang du ikke trenger å beregne sinus. Det er spesielt kompilert Bradis-bord, der alle sines, cosines, tangenter og cotangents allerede er registrert. Herfra mottar vi informasjon. For eksempel, hvis vi kjenner vinkelen, vet vi sin sinus og cosinus. Eller omvendt - hvis en sinus eller cosinus er kjent - kan vi lett finne hvilken vinkel som er gitt.

Naturligvis er disse trigonometriske funksjonene store. Husk dem alt er bare umulig, men egentlig ikke nødvendig. De bruker i hovedsak bare noen av dem.

Litt om hjørnene

Men trigonometriske funksjoner er ikke bareskarpe og rette vinkler, de er også for dumme, men her for å finne dem, er det allerede behov for en sirkel og en graf på koordinataksene. Og dette er en helt annen historie.

sinusoid

La oss nå se hva en sinusoid er. Det ser ut som en sinusoid som dette:

Og er en graf av sinusforandringen iavhengig av vinkelsvingningen. Som nevnt ovenfor kan sidene endres, og vinkelen forblir den samme - da blir sinus uendret. Men hvis vinkelen endres, endres aspektforholdet, og dermed sinusverdien.

Sinusoidet viser numeriske endringer i sinusvinkel og er en graf av funksjonen y = sin (x). Det er ikke noe komplisert her, spesielt siden verdiene til sines av alle vinkler er skrevet i Bradys-tabellene. Men vi vil huske bare de mest grunnleggende.

Litt mer om betegnelsen av vinkler

Alle vet at vinkler måles i grader ellerradianer. Grader vi måler med en grader, som ser ut som en halvcirkel. En grad er 1/360 av en sirkel. Hvorfor så? Fordi en vinkel kan være "åpnet" eller "lukket". Du kan til og med åpne den for hele svingen og få en sirkel.

Full omsetning, som kjent, 360^omtrent. En rett linje er en vinkel på 180^omtrent. Det vil si at diameteren til sirkelen er 180^om. Eller tallet Pi. Derfor viser det seg at vinkelen kan være som 90^omtrent (i grader), og Pi / 2 (i radianer).

Prøv nå å huske de mest grunnleggende bihulene. Hvilke vinkler kommer umiddelbart i tankene?

Direkte vinkel - 90^omtrent, Pi / 2 - sin = 1

Den utfoldede vinkelen er 180^omtrent, Pi - sin = 0

Akutt vinkel på 60^omtrent - Pi / 3 - sin = 0,866

Skarp vinkel 45^omtrent - Pi / 4 - sin = 0,7071