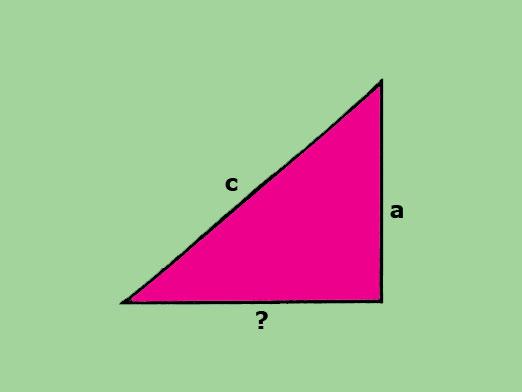Hvordan finner du siden av en riktig trekant?

Geometri er en av de mest komplekse fagene i skolenprogram. Kanskje det vanskeligste for dem som leter etter en løsning på geometriske problemer. I dette tilfellet er den mest korrekte tilnærmingen en klart planlagt algoritme for handlinger. Vel, derfor kunnskapen om formler og teoremer. Når du løser problemer knyttet til søket etter den ukjente siden av en høyre trekant, er det viktig å bruke de første betingelsene og Pythagorasetningen riktig. I tillegg er kunnskap om egenskapene til en rettvinklet trekant viktig. Eksempler på de vanligste betingelsene for problemene i denne serien finner du i denne artikkelen.

La oss finne siden av en riktig trekant

Som kjent er siden av en rektangulærEn trekant kan være en katet eller hypotenuse. Å vite visse forhold, kan du beregne både katetre og hypotenuse, og dermed svare på hovedspørsmålet: Hvordan finne siden av en vinkelret trekant. Vi vurderer disse forholdene og de tilsvarende løsningene.

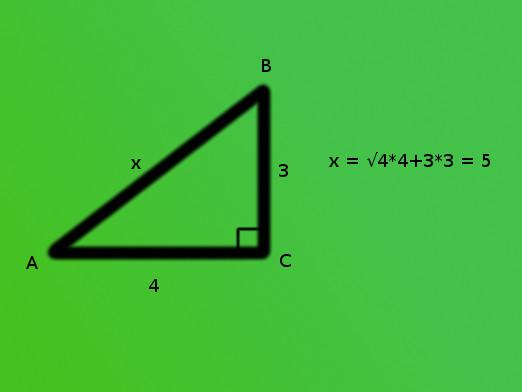
1. Tilstand: Lengden på begge ben er kjent. Hypotenusen kan beregnes ved hjelp av Pythagorasetningen. For de som glemte hva denne setningen er, husk: torget av hypotenus er lik summen av rutene på bena. Gitt den kunnskapen. som ble oppnådd fra teorien, komponerer vi ligningen: FB2 = BK2 + KF2, hvor FB er hypotenuse, og BK og KF er beina. Når du søker etter lengden på hypotenusen, er det nødvendig å firkantet hver av størrelsene på beina igjen. Deretter legger du til de resulterende tallene, og fra resultatet beregner vi kvadratroten.
2. betingelse: Kjent er kateteret og vinkelen som er til den. Denne vinkelen er dannet av hypotenusen og benet som den er festet til. Vi betegner den kjente vinkelen med symbolet a. I samsvar med egenskapen til en høyre trekant skriver vi svaret på denne måten: FB = BK * cos (a)
3. betingelse: Kjent er kateteten (KF) og den samme vinkelen a, som denne tiden er i posisjonen motsatt benet. I midten av hypotenusen i dette tilfellet, vil vi også en rektangulær trekant, som sier at forholdet mellom benet lengde til lengden av hypotenusen er likt med sin motstående side vinkel. Vi skriver det på denne måten: FB = KF * sin (a).
4. Tilstand: Kjent hypotenuse. Ta den rette triangelen ABC, hvor hypotenusen er AC. Vi må angi vinkelen c med toppunktet ved punkt A som La, og vinkelen med toppunktet i punkt B vil bli betegnet av Lb. Deretter må vi finne lengden på bena AB og BC.
5. betingelse: Katete av en riktig trekant er kjent. Vi kan anta at BC er lik b. I dette tilfellet bruker vi teormen til Pythagoras som er kjent for oss (a ^ 2 + b ^ 2 = c ^ 2). Fra ligningen får vi den nødvendige catet | AB | = a = √ (c ^ 2 - b ^ 2).

Å kjenne Pythagoras setning, som du kan se,utfør disse tilsynelatende vanskelige oppgavene i Geometri og forstå selvstendig hvordan du finner siden av en rektangulær trekant, er enkel nok. Hvis du ikke vet, vet du hvordan du bruker Pythagorasetningen, kan du bruke ferdige formler.