Hvordan finner du minst verdien av en funksjon?

Ofte i fysikk og matematikk er det nødvendig å finne minst verdien av en funksjon. Hvordan å gjøre det, vil vi nå fortelle.
Hvordan finne den minste verdien av en funksjon: instruksjon
- For å beregne den minste verdien av en kontinuerlig funksjon i et gitt intervall, må du følge denne algoritmen:
- Finn avledet av funksjonen.
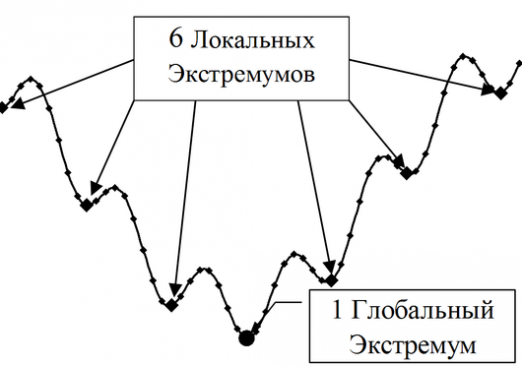
- Finn på et gitt intervall poengene derderivatet er null og alle kritiske punkter. Deretter finner du verdiene av funksjonen på disse punktene, det vil si løse ligningen, hvor x er null. Finn ut hvilken av verdiene som er den minste.
- Bestem hvilken verdi funksjonen har på sluttpunktene. Bestem den minste verdien av funksjonen på disse punktene.
- Sammenlign de mottatte dataene med den minste verdien. Den minste av de oppnådde tallene vil være den minste verdien av funksjonen.
Merk at hvis funksjonen er påSegmentet har ikke minst poeng, det betyr at det på et gitt segment øker eller avtar. Følgelig bør den minste verdien beregnes på endelige segmenter av funksjonen.
I alle andre tilfeller er verdien av funksjonenberegnes av den givne algoritmen. I hvert punkt i algoritmen må du løse en enkel lineær ligning med en rot. Løs ligningen ved hjelp av figuren for å unngå feil.
Hvordan finne den minste verdien av en funksjon påhalvåpent intervall? I den semi-åpne eller åpne perioden av funksjonen, bør den minste verdien bli funnet som følger. På sluttpunktene til verdien av funksjonen, beregne den ensidige grensen for funksjonen. Med andre ord, løse ligningen der de aspirerende punktene er gitt av a + 0 og b + 0, hvor a og b er navnene på de kritiske punktene.
Nå vet du hvordan du finner den minste verdien av en funksjon. Det viktigste er å gjøre alle beregningene riktig, nøyaktig og uten feil.