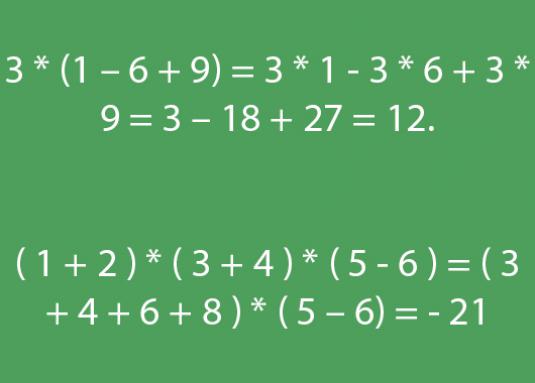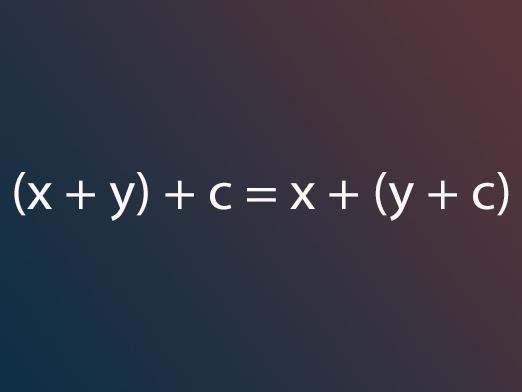Regler for å legge vektorer

For å utføre tilleggsoperasjonenvektorer, det er flere måter, som, avhengig av situasjonen og typen vektorer som anses, kan være mer praktiske å bruke. La oss se på reglene for å legge vektorer:

Regel av trekanten

Regelen av trekanten er som følger: For å legge til to vektorer x, y er det nødvendig å konstruere en vektor x slik at dens opprinnelse sammenfaller med enden av vektoren y. Da vil summen deres være verdien av vektoren z, og opprinnelsen til vektoren z vil falle sammen med begynnelsen av vektoren x og slutten med enden av vektoren y.

Trekantregelen hjelper, hvis antall vektorer som må summeres, er ikke mer enn to.

Regel av et polygon

Polygonregelen er den enkleste og mest praktiskeå legge til et antall vektorer på et fly eller i rommet. Regelenes essens er følgende: Når du legger til vektorer, må du sekvensielt justere dem en etter en slik at begynnelsen av den påfølgende vektor sammenfaller med slutten av den forrige, og vektoren som lukker den formede kurven er summen av vektorene. Dette illustreres grafisk ved ligningen w = x + y + z, hvor vektoren w er summen av disse vektorene. I tillegg bør det bemerkes at summen ikke endres fra endringen i stedene til vektorene, det vil si (x + y) + z = x + (y + z).

Parallellogramregelen

Parallellogramregelen brukes til å legge tilvektorer som stammer fra et enkelt punkt. Denne regelen angir at summen av vektorene x og y, som har en begynnelse på ett punkt blir den tredje vektor z, som stammer også fra dette punkt, og hvor vektorene x og y er sidene i parallellogrammet, og vektoren z - sin diagonal. I dette tilfellet spiller det ingen rolle i hvilken rekkefølge vektorer vil bli lagt til.

Dermed kan polygonregelen, trekantregelen og parallellogramregelen bidra til å løse problemet med å legge vektorer av absolutt kompleksitet, både på flyet og i rommet.