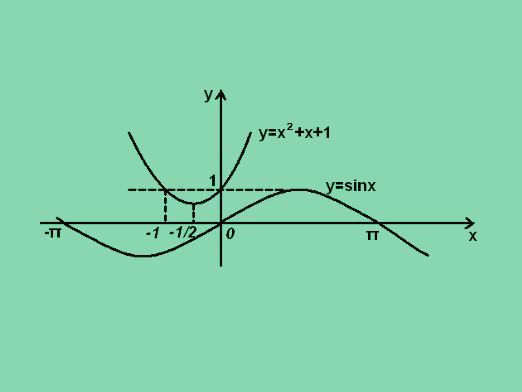
Tilleggsegenskaper

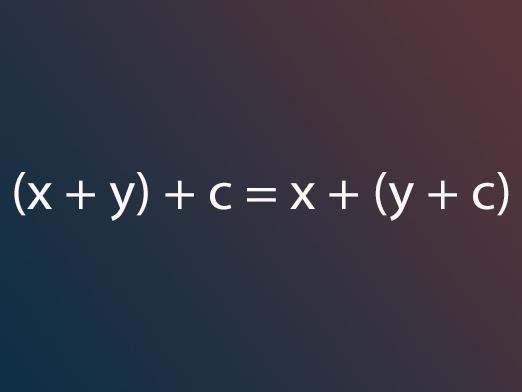
Det er tre egenskaper ved tillegg av tall,som brukes til å løse matematiske problemer, både i enkel og kompleks matematikk. De reisende, kombinere og distribuere eiendommene har sine egne særegenheter og brukes kun når tallene kombineres og multipliseres, og under ingen omstendigheter under noen andre aritmetiske operasjoner.

• Den kombinerende egenskapen ved å legge til tall betyr(x + y) + c = x + (y + c) er sant for alle tallene x, y og c som må legges til. Kombineringsegenskapen som brukes i å multiplisere tall betyr at for alle tallene x, y og c er likestilling (xy) c = x (yc) sant.
• Den flyttbare eiendommen brukes tilTillegg av tallene x og y, indikerer at disse tallene kan omarrangeres i alle retninger, for å gruppere dem i grupper på en måte som er akseptabelt i et bestemt tilfelle, og resultatet vil ikke endres. Fordelingsegenskapen ved tilsetning indikerer at summen oppnådd når to tall legges til, endres ikke dersom disse tallene byttes ut. Følgende ligning brukes: x + y = y + x.
• Distribusjonsegenskapen i tillegg tillater detlegg til tall i henhold til denne ligningen: (x + y) + c = x + (y + c). Den samme egenskapen brukes i multiplikasjon i samsvar med følgende ligning: (xy) c = x (yc). Distribusjonseiendommen gjelder ikke bare når det er nødvendig å multiplisere summen av to summer, men også med summen av tre eller flere vilkår. I dette tilfellet holder likestillingen: x (y + c + d) = xy + xc + xd, uavhengig av hva tallene x, y, c og d er.