Tegn på parallellitet av rette linjer

Parallelliteten til to linjer kan bevises pågrunnlaget for teorien, ifølge hvilken to perpendikulære vinkelrett på en rett linje vil være parallell. Det er visse tegn på parallellitet av linjene - det er bare tre av dem, og alle av dem vil vi vurdere mer spesifikt.
Det første tegn på parallellitet
Rette linjer er parallelle, hvis de er i skjæringen av den tredje rette linjen, vil de dannede indre vinklene som ligger i motsatt retning være like.
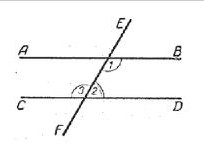
Anta at du krysser linjene AB og CD på linjenved linjen EF ble vinklene I1 og I2 dannet. De er like, siden den rette linjen EF passerer under en skråning i forhold til de andre to rette linjene. Ved krysset av linjer setter vi punktene Ki L - vi har fått et segment av sekant EF. Vi finner midten og legger punktet O (figur 189).

På linjen AB senker vi vinkelrett fra punktet O. Vi kaller det OM. Fortsett vinkelrett til den krysser med den rette CDen. Som et resultat er den opprinnelige linjen AB strengt vinkelrett på MN, noe som betyr at CD_ | _MN, men denne setningen krever bevis. Som et resultat av vinkelrett og skjæringslinjer har vi dannet to trekanter. En av dem er min, den andre er NOC. La oss se nærmere på dem. tegn på parallellitet av linjer 7 klasse
Disse trekanter er like fordi, iI henhold til stedsbetingelsene, / 1 = / 2, og i samsvar med konstruksjonen av trekanter, er siden OK = side OL. Vinkelen MOL = / NOK, siden disse er vertikale vinkler. Fra dette følger at siden og to vinkler ved siden av den av en av trekantene er henholdsvis lik side og to vinkler ved siden av den, den andre av trekanter. Dermed trekant MOL = triangleNOK, og dermed vinkelen LMO = hjørnet av KNO, men vi vet at LMO er rett, derfor er den tilsvarende KNO-vinkelen også en rett linje. Det er klart at vi klarte å bevise det på linjen MN, både linjen AB, og den rette linjens CD er vinkelrett. Det vil si at AB og CD med respekt for hverandre er parallelle. Dette er det vi trengte å bevise. Vurder resterende tegn på parallelle linjer (7. klasse), som avviger fra den første funksjonen ved bevismetoden.
Det andre tegn på parallellitet
Ifølge det andre tegn på parallellitet av rette linjer,vi trenger å bevise at vinklene oppnås i fremgangsmåten til å krysse de parallelle linjene AB og CD direkte EF vil være lik. Således har to parallelle linjer, både den første og den annen likhets er basert på vinklene som oppnås ved skjæringen mellom den tredje linjen. Vi antar at / = 3/2, og vinkel = 1/3 fordi det er loddrett til det. Således er / 2 lik uglu1, men det bør huskes på at den vinkel 1 og 2 vinkel er interne vinkel liggende på tvers. Derfor må vi anvende sine kunnskaper, nemlig at de to segmentene er parallelle, hvis i krysset den tredje rett utdannede, kloke ligger vinkler er like. Dermed har vi funnet at AB || CD.

Vi klarte å bevise at under parallelliseringen av to perpendikulære til en rett linje, i henhold til den tilsvarende setningen, er parallelliteten til linjer tydelig.
Det tredje tegn på parallellitet
Det er også et tredje tegn på parallellisme,som er bevist ved hjelp av en sum av ensidige indre vinkler. Et slikt bevis på linjens parallellitet tillater oss å konkludere at to rette linjer vil være parallelle dersom ved krysset av deres tredje rette linje, summen av de oppnådde ensidige indre vinkler er lik 2d. Se figur 192.