Hvordan finne området på en figur?

Vet og kunne beregne områdene av forskjelligetall er nødvendig for ikke bare å løse enkle geometriske problemer. Ikke gjør uten denne kunnskapen og når du utarbeider eller kontrollerer estimater for reparasjon av lokaler, beregner antall nødvendige forsyninger. Så la oss finne ut hvordan du finner områdene i forskjellige figurer.

område

En del av det plan som omsluttes av den lukkede sløyfen er kalt et område av flyet. Området er uttrykt av antall kvadratiske enheter som er vedlagt den.

For å beregne området for de grunnleggende geometriske figurene må du bruke den riktige formelen.

Arealet av trekanten

Legend:

• S er det nødvendige området,
• a, b, c er lengdene på sidene av trekanten,
• h er høyden på ønsket trekant,
• y er vinkelen mellom side a og side b,
• r er radiusen til sirkelen (innskrevet i en trekant),
• R er radius av sirkelen (beskrevet rundt trekanten),
• p er halvparten av omkretsen av trekanten.

1. Hvis h, a er kjent, er området av den ønskede trekanten definert som produktet av sidelengden og høyden på trekanten droppet til denne siden, delt i halv: S = (a · h) / 2
2. Hvis a, b, c er kjent, så er det nødvendige områdetberegnet av Heron formel: kvadratroten tatt av produktet fra halvparten av omkretsen av trekanten og de tre forskjeller halv og kanten av hver side av triangelet: S = √ (P • (p - a) · (p - b) · (p - c)).
3. Hvis a, b, y er kjent, er området for trekanten definert som halvparten av produkt av 2 sider multiplisert med sinusvinkelverdien mellom disse sidene: S = (a · b · sin γ) / 2
4. Hvis a, b, c, R er kjent, er det ønskede området definert som produktet av lengdene av alle sider av trekanten ved de fire radiusene til den omkretsede sirkelen: S = (a · b · c) / 4R
5. Hvis p, r er kjent, bestemmes det nødvendige område av trekanten ved å multiplisere halvkant av omkretsen ved radiusen til sirkelen som er innskrevet i den: S = p · r

Kvadrat av et torg

Legend:

• S er det nødvendige området,
• a er lengden på siden,
• d er lengden på diagonalen.

1. Hvis siden er kjent, er området av denne figuren definert som kvadratet av sidelengden: S = a²
2. Hvis d er kjent, er kvadratet av torget definert som halve kvadratet av lengden på diagonalen: S = d²/ 2

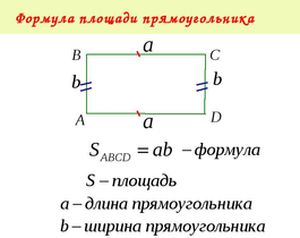
Areal av rektangelet

Legend:

• S er området som skal bestemmes,
• a, b er lengdene på rektangelens sider.

1. Hvis a, b er kjent, bestemmes området av dette rektangel av produktet av lengdene av sine to sider: S = a · b
2. Hvis sidenees lengder er ukjente, må rektangelområdet deles inn i trekanter. I dette tilfellet er rektangelområdet definert som summen av områdene av dets sammensatte trekanter.

Området for parallellogrammet

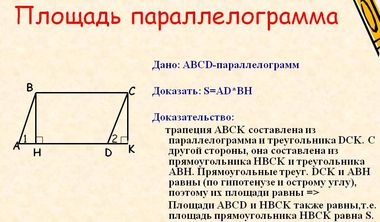
Legend:

• S er det nødvendige området,
• a, b er lengden av sidene,
• h er lengden på høyden til dette parallellogrammet,
• d1, d2 er lengdene på to diagonaler,
• α er vinkelen mellom sidene,
• y er vinkelen mellom diagonalene.

1. Hvis a, h er kjent, bestemmes det ønskede området ved å multiplisere sidelengder og høyden falt på denne siden: S = a · h
2. Hvis a, b, α er kjent, bestemmes området for parallellogrammet ved å multiplisere lengdene på sidene av parallellogrammet og sinusverdien av vinkelen mellom disse sidene: S = a · b · sin α
3. Hvis vi vet d₁, d₂, γ, da er området for parallellogrammet definert som halve produktet av diagonallengder og sinusverdien av vinkelen mellom disse diagonalene: S = (d₁· D₂· Siny) / 2

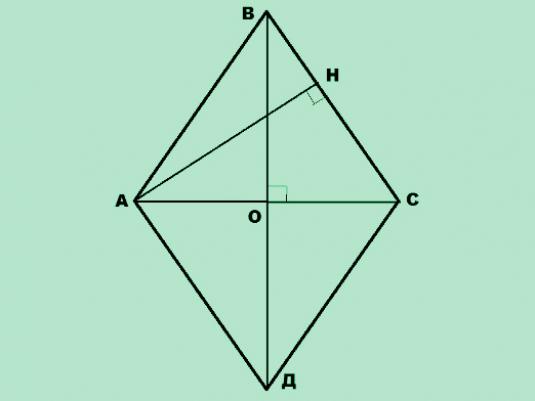
Diamond Square

Legend:

• S er det nødvendige området,
• a er lengden på siden,
• h er lengden på høyden,
• α er den mindre vinkelen mellom de to sidene,
• d1, d2 er lengdene på to diagonaler.

1. Hvis a, h er kjent, bestemmes området av rhombuset ved å multiplisere lengden av siden ved lengden av høyden som senkes til denne siden: S = a · h
2. Hvis a, a er kjent, bestemmes det rombiske området ved å multiplisere kvadratet av sidelengden ved sinus av vinkelen mellom sidene: S = a²· Sin a
3. Hvis vi vet d₁ og d₂, så er det nødvendige området definert som halve produktet av lengdene på diamanter i rhombuset: S = (d₁· D₂) / 2

Trapesområde

Legend:

• S er det nødvendige området,
• a, b - lengder på 2 baser av trapesen,
• c, d er lengdene til venstre og høyre side av trapesformet,
• h er høyden på trapesformet,

1. Hvis a, b, c, d er kjent, er det nødvendige området bestemt av formelen: S = (a + b) / 2 * √ [c²- (((b-a)²+ c²-d²) / (2 (b-a))²].
2. For kjent a, b, h er det nødvendige området definert som produktet av halv summen av basene og trapeshøyden: S = (a + b) / 2 · h

Areal av en konveks firkant

Legend:

• S er det nødvendige området,
• d₁, d₂ - lengdene på diagonaler av en gitt firkantet,
• α er vinkelen mellom diagonalene,
• p = (a + b + c + d) / 2 er halvparten av omkretsen av den konvekse firkanten,
• a og b, c og d er lengdene på hver side av den konvekse firkanten,
• θ = (α + β) / 2 er halvparten av summen av to motsatte vinkler av en konveks firkant,
• r er sirkelens radius innskrivet i en konveks firkant.

1. Hvis vi vet d₁, d₂, a, da er området for den konvekse firkanten definert som halvparten av diagonalene av firkanten multiplikert med sinusvinkelen mellom disse diagonalene: S = (d₁· D ₂· Sin a) / 2
2. For kjent p, r, er området av det konvekse firkantet definert som produktet av semipimeteret av firkanten ved radiusen til sirkelen som er innskrevet i denne firkantet: S = p · r
3. Hvis a, b, c, d, θ er kjent, så er det konvekse områdetfirkantet er definert som kvadratroten av produktene av forskjellen i halvperimeteren og lengden på hver side minus produktet av lengdene på alle sider og cosinusfeltet av halvparten av to motstående vinkler: S² = (p - a) (p - b) (p - c) (p - d) - abcd · cos²((a + β) / 2)

Sirkelområde

Legend:

• S er det nødvendige området,
• r er lengden på radiusen,
• d er lengden på diameteren.

Hvis r er kjent, er det ønskede området definert som produktet av tallet π av radiusen i kvadratet: S = π r²

Hvis d er kjent, er sirkelområdet definert som produktet av tallet π ved kvadratet av diameteren, dividert med fire: S = (π · d²) / 4

Området med en kompleks figur

En kompleks en kan deles inn i enkle geometriske figurer. Arealet av en kompleks figur er definert som summen eller forskjellen på de aktuelle områdene. Tenk for eksempel en ring.

betegnelse:

• S er ringenes område,
• R, r er radien til den ytre omkretsen og innvendig, henholdsvis,
• D, D - diameter av henholdsvis den ytre omkrets og indre.

For å finne ringenes område er det nødvendig å ta området

mindre sirkel. S = S1-S2 = πR²-πr² = π (R²-r²).

Således, hvis R og r er kjent, er ringenes område definert som forskjellen på firkantene av radiene til ytre og indre sirkler multiplisert med tallet pi: S = π (R²-r²).

Dersom det er kjent D og d, er ringen området som defineres som en fjerdedel av differansen av kvadratene av diametrene av de ytre og indre omkrets, multiplisert med pi: S = (1/4) (D²-d²) π.

Området av den skyggefulle figuren

Anta at det er en annen (B) (mindre) inne i samme firkant (A), og vi må finne den skyggefulle hulrommet mellom tallene "A" og "B". La oss bare si "rammen" av et lite torg. For å gjøre dette:

1. Vi finner området i figuren "A" (beregnet av formelen for å finne plassen på plassen).
2. På samme måte finner vi området i figuren "B".
3. Vi trekker område "B" fra område "A". Og så får vi området til den skyggefulle figuren.

Nå vet du hvordan du finner områder av forskjellige former.