Hvordan finne området for en parallellpiped?

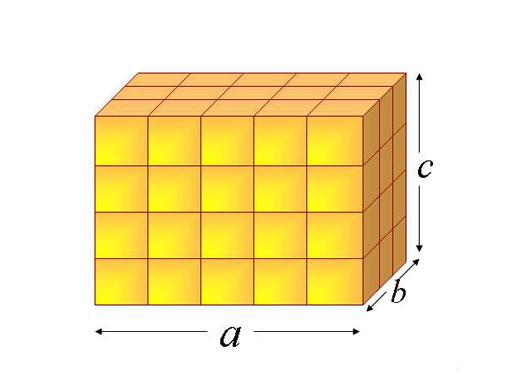
I den geometriske figuren har parallellpipedeneseks ansikter - fire grunnleggende og to baser (per definisjon er de alle parallellogrammer). Hvis alle seks er rektangler, vil parallellpipedelen være en rett linje. Kantene på motsatte sider er like, og de er parallelle. De fire diagonaler av parallellpipedene konvergerer på et enkelt punkt og deler i to.

For å finne ut hvordan du finner et områdeDet er nødvendig å beregne først arealet av alle dens baser (betegnet med bokstaven -a), dets sideveis (betegnet med bokstaven -b), mens du bestemmer lengden av basen og kanten.

Først tegner vi høyden på parallellogrammet (betegnet ved bokstaven - h), deretter kanten til parallellpiped (angitt ved bokstaven - H). Eller gjennom sidens lengder (a, b, c).

Det totale arealet av basene er: S = 2a * h eller S = 2ac

Siden sideflatene er rektangler, er deres område: S = 2a * H og S = 2b * h eller S = 2a * b, S = 2b * c

Derfor fant vi ut hvordan vi skulle finne områdetcuboid - endelig beregning formel skrives som: S = 2AH + 2 Ah + 2BH = 2 (ah + aH + BH) eller S = 2 (Sa + Sb + Sc) = 2 (ab + bc + ac), nemlig det dobbelte av summen av arealene ansikter av en parallellpiped.

Det er tilfeller når siden vender utParallellogrammet ligger i en hvilken som helst vinkel mot basen, så parallellpiped er tilbøyelig. Deretter beregnes området av sidevinklene ved å kjenne deres høyde. I dette tilfellet beregnes området av basene identisk.

Ingenting komplisert.