Hvordan løse ulikheter?

Ikke alle vet hvordan å løse ulikhetene somderes struktur har lignende og særegne egenskaper med ligningene. Ligningen er en øvelse som består av to deler, mellom hvilke det er et likestilt, og mellom ulikhetens deler kan det være et tegn "mer" eller "mindre". Derfor må vi forstå at det er nødvendig å ta hensyn til tegn på et tall (positivt eller negativt) før det blir nødvendig å formere begge deler med et uttrykk før vi finner en løsning på en bestemt ulikhet. Det samme skal tas hensyn til dersom det er nødvendig å kvadre løsningen av ulikheten, da kvadrering utføres ved multiplikasjon.
Hvordan løse systemet med ulikheter
Det er mye vanskeligere å løse ulikhetssystemer ennVanlige ulikheter. Hvordan løse ulikheten i 9. klasse, vil vi vurdere med konkrete eksempler. Det skal forstås at før det løses kvadratiske ulikheter (systemer) eller andre ulikheter, er det nødvendig å løse hver ulikhet separat, og deretter å sammenligne dem. Løsningen av ulikhetssystemet er enten et positivt eller et negativt svar (systemet har en løsning eller har ingen løsning).
Oppgaven er å løse et sett av ulikheter:

Vi løser hver ulikhet separat

Vi konstruerer en numerisk linje som vi representerer settet av løsninger
svare:

Siden samlingen er en sammenslutning av sett med løsninger, må dette settet på nummerlinjen understrekes av minst en linje.
Løsning av ulikheter med en modul
Dette eksemplet viser hvordan ulikheter løses med modulen. Så, vi har en definisjon:

Vi må løse ulikheten:
| x |> 2
Før du løser en slik ulikhet, er det nødvendig å kvitte seg med modulen (tegn)
La oss skrive, basert på definisjonen:

eller

Nå er det nødvendig å løse hvert av systemene separat.
Vi konstruerer en numerisk linje som vi representerer sett med løsninger.
Som et resultat har vi fått et sett som forener mange løsninger.
svare:

Løsning av kvadratiske ulikheter
Bruk den numeriske rette linjen, vurder løsningen av kvadratiske ulikheter. Vi har ulikhet:
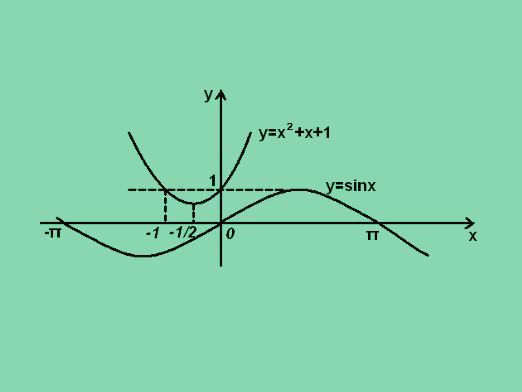
Vi vet at grafen til en kvadratisk trinomial er en parabola. Vi vet også at grenene til en parabola er rettet oppover, hvis en> 0.
x2-3x-4 <0
Ved hjelp av Viets setning finner vi røttene x1 = - 1; x2 = 4
Vi tegner en parabola, eller rettere, en skisse.
Dermed fant vi ut at verdiene til det kvadratiske trinomialet vil være mindre enn 0 på segmentet fra-1 til 4.
svare:
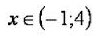
Mange spørsmål oppstår når du løser dobbelulikheter av typen g (x) <f (x) <q (x). Før du løser dobbelt ulikheter, er det nødvendig å dekomponere dem til enkle, og løse hver enkelt av de enkle ulikhetene separat. For eksempel, å utvide vårt eksempel, får vi som et resultat et system med ulikheter g (x) <f (x) og f (x) <q (x), som skal løses.
Faktisk finnes det flere metoder for å løse ulikheter, så du kan bruke den grafiske metoden for å løse komplekse ulikheter.
Løsning av fraksjonelle ulikheter
En mer grundig tilnærming krever fraksjonulikhet. Dette skyldes det faktum at skiltet kan endres i prosessen med å løse visse brøkdelingsforskjeller. Før det løses brøkdelingsforskjeller, er det nødvendig å vite at intervallmetoden brukes til å løse dem. Den brøkdelige ulikheten må være representert på en slik måte at den ene siden av tegnet ser ut som et brøk-rasjonelt uttrykk, og det andre - "-0". Ved å omforme ulikheten på denne måten får vi som følge f (x) / g (x)> (.
Løse ulikheter etter intervallmetoden
Intervallteknikken er basert på fullføringsmetodeninduksjon, det vil si å finne alle mulige varianter for å finne løsningen av ulikheten. Denne løsningsmetoden vil kanskje ikke være nødvendig for studenter i 8. klasse, siden de trenger å vite hvordan de skal løse de 8. klasse ulikhetene, som er de enkleste øvelsene. Men for eldre klasser er denne metoden uerstattelig, siden det bidrar til å løse fraksjonelle ulikheter. Løsningen av ulikheter ved hjelp av denne teknikken er basert på egenskapen til en kontinuerlig funksjon, for eksempel bevaring av tegnet mellom verdiene der det blir 0.
Vi konstruerer grafen av polynomet. Dette er en kontinuerlig funksjon som oppnår en verdi på 0 3 ganger, det vil si f (x) blir 0 ved punktene x1, x2 og x3, røttene til polynomet. I mellom disse punktene blir tegn på funksjonen bevart.
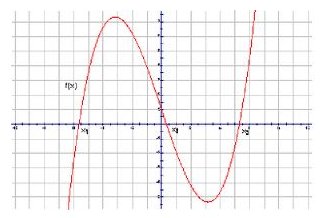
Siden å løse ulikheten f (x)> 0 trenger vi et funksjonsmerke, gå til koordinatlinjen, og la grafen gå.

f (x)> 0 for x (x1; x2) og for x (x3; )
f (x) x (-; x1) og for x (x2; x3)
Grafen viser tydelig løsningene på ulikheterf (x) f (x)> 0 (blå for første ulikhet og rød for den andre). For å bestemme For å bestemme tegnet på en funksjon i et intervall, er det tilstrekkelig at du vet tegn på en funksjon på et av punktene. Denne teknikken gjør at vi raskt kan løse ulikheter der venstre side er faktorisert, fordi det er lett nok å finne røtter i slike ulikheter.