Hvordan finner du et rektangelområde?

Ordet "geometri" i oversettelse betyr "landmåling": "Geos" på gresk er jord, og "metry" er en måling. Selv de gamle egypterne, tusenvis av år før vår tid, måtte revurdere og dele land etter flomene av de store elvene i Nilen, Eufraten eller Tigrisen. Det var umulig å gjøre uten presis matematisk kunnskap. Så det var en vitenskapsgeometri, rent anvendt, for å løse praktiske problemer. Definisjonen av områdene i ulike tall var relevant for de hasteroppgaver, fordi arealet var av forskjellige størrelser og former. I Russland ble det i 1629 publisert "Sick Letter", der det ble angitt metoder for måling av polygonområdene. Vi bruker formlene beskrevet i boken i dag.

For å forstå hvordan du finner området i et rektangel,Det er nødvendig å definere begrepet "område". Hver geometrisk figur er preget av en rekke mengder, hvorav en er området. For en flat figur er området hovedkarakteristikken. Hvis vi deler figuren i firkanter med en sidelengde som er lik en og beregner deres totale tall, så får vi området til den oppgitte figuren. Måleenheten av området i det internasjonale metriske SI-systemet er en kvadratmeter.

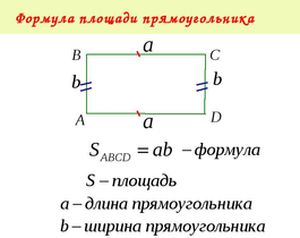
Husk at et rektangel kallesfirkantet med fire rette vinkler. Dimensjonene av rektangelet bestemmes av lengden av sidene, som vanligvis er betegnet med de latinske bokstavene a og b. Vanligvis tar vi størrelsen på den ene siden av rektangelet i lengden, og den andre for bredden eller høyden. Så hvordan finner du området av rektangelet? Vi må vite lengden og bredden, det vil si størrelsen på sidene. Hvis vi dekke overflaten av det rektangulære gitter av kvadrater med en side av aggregatet (1 cm, 1 mm, 1 meter ...) og beregne disse små firkanter, får vi en verdi som er lik produktet av antall ruter, store til å passe langs den ene side av rektangelet, og deres antall langs den andre siden. Denne mengden er det nødvendige området. Det vil si at formelen for å finne området av et rektangel ser slik ut:

S = (a) * (b)

hvor a er lengden av rektangelet, b er bredden (eller høyden) av rektangelet.

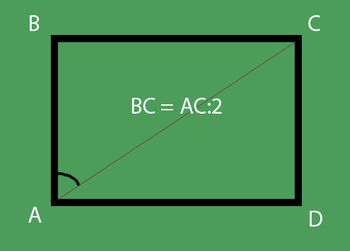
Forresten, siden hver diagonal deler segrektangel i to like rektangulære trekanter, så kan rektangelområdet også bestemmes ved å telle området for en slik trekant og multiplisere resultatet med to. Du trenger bare å kjenne formelen for triangelområdet, men dette er en helt annen historie!