Hvordan runde tall?

Avrundingstall er den enkleste matematiske operasjonen. For å kunne ringe tallene riktig må du vite tre regler.

Regel 1

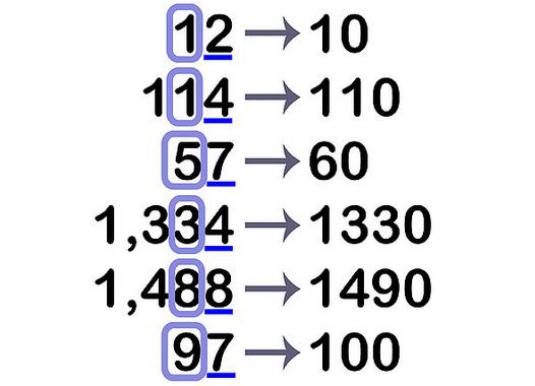
Når vi ringer opp et tall til et visst nivå, må vi kvitte oss med alle sifrene til høyre for denne rangen.

For eksempel må vi runde tallet 7531 til hundrevis. I dette nummeret fem hundre. Til høyre for dette sifferet er det tallene 3 og 1. Vi setter dem til nuller og får nummeret 7500. Det er å avrunde tallet 7531 til hundrevis, vi fikk 7500.

Når du avrunder de brøkdelte tallene, skjer alt slikBare overflødige utslipp kan enkelt slippes. La oss si at vi må runde nummeret 12.325 til tiende. For å gjøre dette, etter kommaet, må vi legge et siffer - 3, og alle tallene til høyre, kaste bort. Resultatet av å avrunde nummeret 12.325 til tiende er 12,3.

Regel 2

Hvis det kasserte sifferet til høyre for venstre siffer er 0, 1, 2, 3 eller 4, endres ikke figuren vi forlater.

Denne regelen fungerte i de to foregående eksemplene.

Så når du ringer nummeret 7531 til hundrevis av seg selvnær tallet som var igjen fra kasserte var en trippel. Derfor har figuren vi forlot - 5 - ikke endret seg. Avrundingsresultatet er tallet 7500.

Tilsvarende, når nummeret er avrundet 12.325 tilDet tiende sifferet, som vi droppet etter triplen, var en to. Derfor endret høyre side av venstre siffer (trippel) ikke ved avrunding. Det var 12,3.

Regel 3

Hvis venstre side av de kasserte sifrene er lik 5, 6, 7, 8 eller 9, økes sifferet som vi runder opp med en.

For eksempel må du rulle nummeret 156 til dusinvis. I dette antallet 5 dusinvis. I kategorien av enheter, hvorfra vi kommer til å bli kvitt, er det en tall på 6. Derfor må tiene tallet økes med en. Derfor, når vi runder tallet 156 til tiere, får vi 160.

Tenk på et eksempel med et brøknummer. For eksempel går vi rundt 0.238 til hundre. Ved regel 1 må vi slippe de åtte, som står til høyre for hundre klasse. Og i henhold til regel 3 må vi øke topp tre i hundrevis av en. Som et resultat, avrunde antallet 0,238 til hundre, får vi 0,24.