Hvordan beregne en kube?

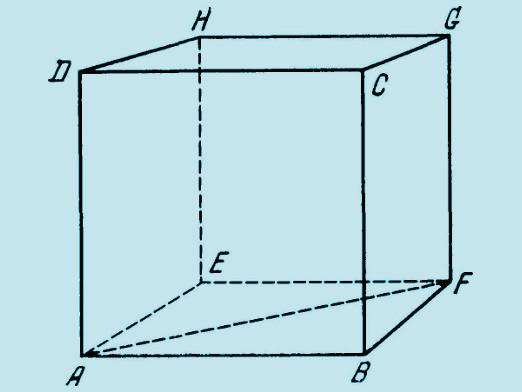
Først av alt, for å forstå hvordan å beregne områdetkube, du trenger å vite hva slags figur det er, hvilke funksjoner og egenskaper den har. Fordi du vet hva kuben er og hva dens hovedkomponenter er, desto lettere blir det å beregne denne geometriske figuren. Så er en terning en vanlig polyhedron, og hver av ansiktene er en firkant. Kubens kanter er seks. Også private kube tilfeller er: et prisme og parallellepipediske former eller polyhedrons data, har andre komponenter, dvs. kombinerer prisme deres ansikter lik polygoner, parallellogrammer, og som for boksen - her en klar parallellogram. Før vi beregner en kube, vil vi forholde oss til dens egenskaper:

1. Tverrsnitt av terningen er sekskanter.
2. En kube diagonal er et segment som forbinder to toppunkter, og de er i sin tur symmetriske til midten av terningen.
3. Vi gir hovedformlene for å løse denne figuren:

• Kubens område - 6a² ;
• Volumet er - a³ ;
• Radens sfære som er innskrevet i terningen er 1/2 * a;
• Radens sfære som er beskrevet er - roten med 3 divisjonert med 2 og multiplisert med "a".

Instruksjoner for beregning av terningen

Siden spørsmålet lyder for oss: hvordan å beregne en terning, la oss se på trinn-for-trinns instruksjon om hvordan du beregner denne geometriske figuren:

1. Etter at vi funnet ut hva som erterning, hva den har funksjoner, formler for å beregne hovedkomponentene, er det nødvendig å akseptere beregninger. Først og fremst må du være oppmerksom på hvilken informasjon du har (sidens dimensjoner, diagonalens lengde), hvis det ikke er noen informasjon, så skal det gjøres ganske enkelt - navnet på kanten av kuben "a". Videre i beregningene, start fra denne bokstavsverdien.
2. Deretter begynner du å spole ut beregningene dine, somtangle av tråd. Hvis en kant av kuben er "a", så er noen andre også "a". Deretter må du beregne ansiktets område, og ansiktet er det samme vanlige torget - kvadratet av torget som er kjent for alle². Diagonal kube er heller ikke vanskelig å måle medVed hjelp av Pythagorasetningen, som tilsvarer "a", multipliseres med kvadratroten til de to. Husk at omtrent en kube, dette er et volumetrisk torg, og beregner en du vil få nesten alt.
3. Nå kan vi gå videre til andre beregninger, for eksempel kubens område, som vi allerede nevnte ovenfor, er 6a². Det vil si å kjenne området med ett ansikt - vi finner området og hele kuben. Nesten samme måte, kan vi finne volumet av terningen. Ut fra det faktum at volumet er lik a³, så er alle sider lik verdien av "a", noe som betyr at kubens volum ikke kan bli funnet enkelt.

Så her er en enkel måte du lærte hvilke handlinger du må ta for å beregne hvilken som helst kube. Prøv det, eksperiment!