Konstruer en graf rett?

Matematikk - vitenskapen er ikke lett, og ikke alleer gitt fra første gang. Noen ganger sitter elevene for abstrakter i flere timer for å endelig forstå hvordan man bygger en direkte graf, selv om det i virkeligheten ingenting er komplisert her: du trenger bare å nøye forstå alle elementene i ligningen og forstå teknologien for å løse ligningen som du kan bygge på grafen i form av en rett linje.

En graf på den enkle ligningen

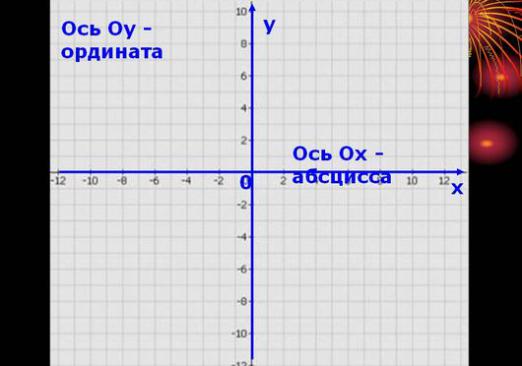
Den enkleste ligningen som den er ønskelig pålær å bygge rette linjer på grafen - dette er y = kx + b. I dette tilfellet er det klart at y avhenger lineært på x, og løsningen til ligningen kan bestemmes grafisk. For å gjøre dette velger vi først to punkter på en rett linje og kaller dem A og B. For å unngå å lide lenge i konstruksjonen, er det best å sette disse punktene på kryssene med aksene.

Bestemmelse av koordinater

Nå må vi avgjøre hvilke koordinaterdet er disse punktene. For å gjøre dette, faller vi vinkelrette linjer fra punkter til koordinataksen. Tallene på skalaen er koordinatene til punktene A og B. For eksempel koordinatene til punktet A - (2; 3) og punktene B - (-2; 0). Etter dette erstatter vi de innhentede dataene i den generelle ligningen. Så for A får vi 3 = 2k + b, og for punkt B - 0 = -2k + b. Følgelig har vi et system med to ligninger, hvor de ukjente er k og b.

Løsning av systemet av ligninger

1. Et slikt system kan løses av noe som passer degmåte. I tilfellet av eksemplet kan to likninger legges til, siden i begge deler av systemet er koeffisienten k ukjent, og de gjenværende koeffisientene er like i absolutt verdi, selv om de er motsatte i tegnet. Da får vi det 3 + 0 = 2k - 2k + b + b. Vi forenkler ligningen og får 2b = 3. Derfor får vi det b = 3/2. Deretter erstattes denne verdien av elementet b i en hvilken som helst ligning og finner k. Vi får: 0 = -2k + 3/2, hvorfra vi uttaler at k = 3/4.
2. Nå kan vi erstatte verdiene for koeffisientene k og b i den opprinnelige ligningen, og få ligningen til den rette linjen som vi burde ha funnet. Så, det ser ut som y = 3x / 4 + 3/2.

Ved dette prinsippet, nesten noenlineær ligning. Algoritmen forblir den samme - bare variablene endres. Hovedinnholdet i denne form for lineære ligninger er å tegne en graf riktig og spesifisere poeng. Etter dette forblir det bare å bestemme koordinatene og erstatte dataene i ligningen, og utgjør systemet. Koeffisienten k er hellingen til den rette linjen. Trigonometrisk, denne koeffisienten kan defineres som tangent av vinkelen mellom x-aksen og den rette linjen. Den ukjente y i en slik ligning er en variabel, akkurat som x.

Hvis, selv ved hjelp av de ovennevnte instruksjonenefor å bestemme ligningen for den rette linjen virker ikke, så kan du bruke funksjonen til å bygge en online graf av linjen. På Internett kan du finne mange steder der det er nok å legge inn ligningen som er gitt til deg, og etter noen få øyeblikk får du en komplett løsning, et klart diagram og en endelig ligning.

Du trenger bare å skrive om detteautomatisk beslutning i en notatbok, men det er selvsagt bedre å håndtere løsningen av slike ligninger uavhengig, siden matematikk er en svært viktig vitenskap, uten hvilken ingen beregninger kan eksistere. Derfor anbefaler vi deg å forstå og forstå konstruksjonen av grafer og løsningen av lineære ligninger.