Hvordan finne den midtre trapesformede linjen?

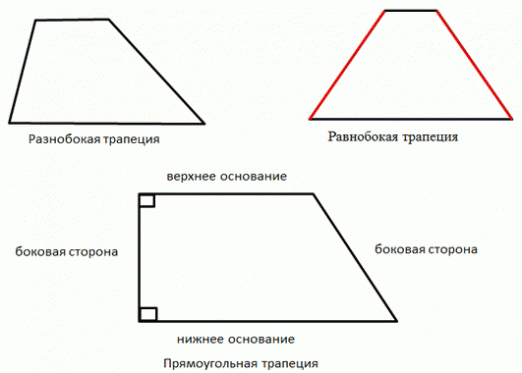
Et segment av en rett linje som forbinder midten av lateralsider av trapesformen, kalles trapesens midtlinje. Hvordan finne den midtre trapeslinjen og hvordan den relaterer seg til andre elementer i denne figuren, vil vi diskutere nedenfor.

Midtlinjesetningen

Tegn en trapezoid der AD er en størrebase, BC - mindre base, EF - mellomlinje. Vi fortsetter grunnlaget AD for punkt D. Tegn linjen BF og fortsett den til den krysser med fortsettelsen av basisannonsen ved punktet O. Tenk på trianglene ΔBCF og ΔDFO. Vinkler ∟BCF = ∟DFO som vertikal. CF = DF, ∟ BCF = ∟ FDO, fordi ВС // АО. Derfor trekantene ΔBCF = ΔDFO. Dermed sidene BF = FO.

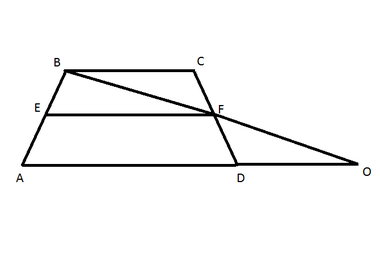
Nå vurder ΔABO og ΔEBF. ∟ABO er vanlig for begge trekanter. BE / AB = ½ etter betingelse, BF / BO = ½, siden ΔBCF = ΔDFO. Følgelig er trianglene ABO og EFB like. Dermed er forholdet mellom sidene EF / AO = ½, samt forholdet mellom de andre partene.

Vi finner EF = ½ AO. Det kan ses fra tegningen at AO = AD + DO. DO = BC som sidene av like trekant, dermed AO = AD + BC. Derfor er EF = ½ AO = ½ (AD + BC). dvs. Lengden på trapesens midtre linje er lik halvparten av basene.

Er midtlinjen av trapesen alltid lik halvparten av basene?

Anta at det finnes et spesielt tilfelle,når EF ≠ 1 (AD + BC). Så BC ≠ DO, derfor, ΔBCF ≠ ΔDCF. Men dette er umulig, fordi de har to like vinkler og sider mellom dem. Følgelig er setningen sant under alle forhold.

Midtlinjen problemet

Anta at i den trapesformede ABCD AD / BC, ∟A = 90 °, ≡C = 135 °, AB = 2 cm, er diagonal AC vinkelrett på sidesiden. Finn den midtre trapesformede linjen EF.

Hvis ∟A = 90 °, så ∟B = 90 °, så er ΔABC rektangulær.

∟ BCA = ∟BCD - ∟ACD. ∟ACD = 90 ° etter tilstand, derfor, ∟BCA = ∟BCD - ACACD = 135 ° - 90 ° = 45 °.

Hvis i en rektangulær trekant ΔABC er en vinkel 45 °, da er beina i den lik: AB = BC = 2 cm.

Hypotenus AC = √ (АВ² + ВС²) = √8 cm.

Vurder ΔACD. ACACD = 90 ° etter tilstanden. ∟CAD = ∟BCA = 45 ° som vinklene dannet av trapesens sekantiske parallelle baser. Følgelig benene AC = CD = √8.

Hypotenus AD = √ (AC² + CD²) = √ (8 + 8) = √16 = 4 cm.

Den gjennomsnittlige trapeslinjen er EF = ½ (AD + BC) = ½ (2 + 4) = 3 cm.